2017-06-28

pythonで正規性の検定【コロモゴロフスミルノフ検定（KS検定）】

統計

確率分布が正規分布に従うか調べたい、
二つの集団が同じ確率分布から得られたものか調べたい、
といった時に使うのが、コロモゴロフスミルノフ検定(Kolmogorov–Smirnov test)

コルモゴロフ–スミルノフ検定（コルモゴロフ–スミルノフけんてい、英: Kolmogorov–Smirnov test）は統計学における仮説検定の一種であり、有限個の標本に基づいて、二つの母集団の確率分布が異なるものであるかどうか、あるいは母集団の確率分布が帰無仮説で提示された分布と異なっているかどうかを調べるために用いられる。しばしばKS検定と略される。
1標本KS検定は、経験分布を帰無仮説において示された累積分布関数と比較する。主な応用は、正規分布および一様分布に関する適合度検定である。正規分布に関する検定については、リリフォースによる若干の改良が知られている（リリフォース検定）。正規分布の場合、一般にはリリフォース検定よりもシャピロ-ウィルク検定やアンダーソン-ダーリング検定の方がより強力な手法である。
2標本KS検定は、二つの標本を比較する最も有効かつ一般的なノンパラメトリック手法の一つである。これは、この手法が二つの標本に関する経験分布の位置および形状の双方に依存するためである。
wikipedia:コルモゴロフ-スミルノフ検定

pythonではscipyで用意されている。

1標本の場合

from scipy import stats
stats.kstest(rvs, cdf, args=(), N=20, alternative='two-sided', mode='approx')

rvs:データor単語
cdf:累積分布
args:分布の形状を指すパラメータ（必要に応じて）

p値はpvalueで取り出す。

試してみる

正規分布
コーシー分布
t分布（自由度３）

の3つに対して、正確に分けられるかチェック。
正規分布のデータは正規分布だと、そうでないデータは正規分布ではないと判別してほしい。

x = stats.norm.rvs(size=500)
y = stats.cauchy.rvs(size=500)
z = stats.t.rvs(3,size=500)
print(stats.kstest(x,"norm").pvalue)
print(stats.kstest(y,"norm").pvalue)
print(stats.kstest(z,"norm").pvalue)

0.611401246262    #正規分布(>0.05)
8.59754489824e-11 #コーシー分布(<0.05)
0.0135550060406   #t分布(<0.05)

正規分布とそうでない分布がきちんと判別できていることがわかる。
※帰無仮説の本来の意味からもわかるように、p値が基準値を下回らなくても正規分布と断定することはできないことに注意。

【補足】KS検定 vs. シャピロ-ウィルク検定

正規性の検定に限っては、wikipediaに載っているようにシャピロウィルク検定が良いらしい。
幸いscipyで実装されているようだったので、試してみる。

>>> from scipy import stats
>>> np.random.seed(12345678)
>>> x = stats.norm.rvs(loc=5, scale=3, size=100)
>>> stats.shapiro(x)
(0.9772805571556091, 0.08144091814756393)

方法

性能を比較するため、サンプルサイズを25～500の間を25刻みで増やしていく。
コーシー分布、t分布(自由度3)、正規分布のそれぞれの分布・サンプルサイズに対して40回のサンプリングを行い、得られたp値の平均値をプロットする。
どれくらいのサンプルサイズだと誤判別が起きないかを確認してみる。有意水準は95%とした。

1. コロモゴロフスミルノフ検定

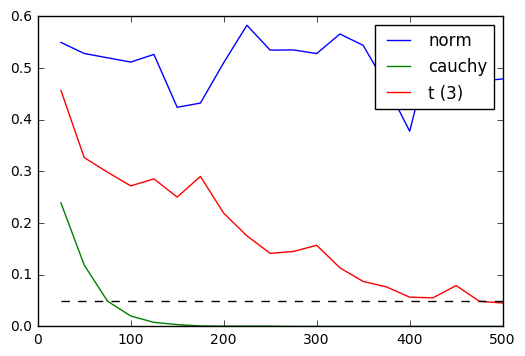
2. シャピロウィルク検定

コーシー分布・ｔ分布のどちらともが点線（5％）を下回っていれば判別できている（正規分布ではないと判断している）ということだが、シャピロウィルク検定はサンプルサイズが小さくてもよく判別できているといえる。
シャピロウィルク検定の場合サンプルサイズが100程度あれば十分かも。
また、どちらの検定でも正規分布なのに正規分布でないと判断してしまうことはなかった。

使ったコード

samplesize = range(25,525,25)
samplingnum = 40
xlist = []
ylist = []
zlist = []
for i in samplesize:
    xsampling = []
    ysampling = []
    zsampling = []
    for j in range(samplingnum):
        x = stats.norm.rvs(size=i)
        y = stats.cauchy.rvs(size=i)
        z = stats.t.rvs(3, size=i)
        xsampling.append(stats.shapiro(x)[1])
        ysampling.append(stats.shapiro(y)[1])
        zsampling.append(stats.shapiro(z)[1])
    xlist.append(sum(xsampling)*1.0/samplingnum)
    ylist.append(sum(ysampling)*1.0/samplingnum)
    zlist.append(sum(zsampling)*1.0/samplingnum)
plt.plot(samplesize,xlist, label="norm")
plt.plot(samplesize,ylist, label="cauchy")
plt.plot(samplesize,zlist, label="t (3)")
plt.plot(samplesize,[0.05 for i in range(len(samplesize))], "--", color="black")
plt.legend()
plt.show()

2標本の比較

from scipy import stats
stats.ks_2samp(data1, data2)

データサイズは違っても構わない。

試してみる

①コーシー分布とコーシー分布
②コーシー分布とt分布（自由度３）
で比べてみる

y = stats.cauchy.rvs(size=500)
y1 = stats.cauchy.rvs(size=500)
z = stats.t.rvs(3, size=500)
print(stats.ks_2samp(y,y1).pvalue)
print(stats.ks_2samp(y,z).pvalue)

0.655550311167  # コーシー分布vsコーシー分布(>0.05)
0.022458470313  # コーシー分布vsｔ分布(<0.05)

5％の基準だと、きちんと判別できている。

公式サイト：
scipy.stats.shapiro — SciPy v0.19.0 Reference Guide
scipy.stats.kstest — SciPy v0.14.0 Reference Guide
scipy.stats.ks_2samp — SciPy v0.15.1 Reference Guide

2017-06-26

二項分布の極限が正規分布になることの証明【正規近似の証明】

数学統計

二項分布の試行回数を無限大に大きくしていくと正規分布に近づくことが知られている。
しかし、その証明は意外と知られていない。（中心極限定理でも証明は可能ではあるが、回りくどすぎて初学者には不親切）

$e$ や $\pi$ が出てくるのがどうしても不思議で、自分なりに解こうとしたり調べてみた。
ようやくわかってきたので、自分的にわかりやすかった方法を記録しておく。
ただ、これはわかりやすさ重視の証明法らしい。
数学的に厳密じゃないところとか突っ込んでくれると嬉しいです。

予備知識

二項分布 : $\displaystyle B(n,p)={}_n C_{x} p^x(1-p)^{n-x}$

正規分布 : $\displaystyle \mathcal{N}(\mu,\,\sigma^{2}) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(\mu - x)^2}{2\sigma^2}\right)$

二項分布の正規近似 : $\displaystyle \lim_{n \to \infty} B(n,p)=\mathcal{N}(np,\,np(1-p))$

証明

方針

二項分布の対数をとった関数をTaylor展開し二次の項まで近似すると正規分布の対数になることを示す。

証明

二項分布の自然対数をとる．
$\displaystyle \begin{equation} \begin{split} \log{B(n,p)} &= \log{{}_n C_{x} p^x(1-p)^{n-x}}\\ &= \log{\frac{n!}{x!(n-x)!} p^x(1-p)^{n-x}}\\ &= \log{n!} - \log{x!} - \log{(n-x)!} + x\log{p} + (n-x)\log{(1-p)}　 \end{split} \end{equation}$
ここでTaylor展開を考えるにあたり，
$\log{x!},\, \log{(n-x)!}$
の項について考える．

補題として，
[補題１]
充分に大きい自然数 $k$ に対して
$\displaystyle \log{k!} \simeq \int_1^k\log{t} dt$
が成り立つことを示す。
[補題１証明]
2以上の自然数 $a$ に対して， $\log{(t)}$ は単調増加であるので
$\displaystyle \log{(a-1)} < \int_{a-1}^a \log{t} dt < \log{a}$
が成り立つ．
したがって
$\displaystyle \begin{equation} \log{(k-1)!} < \int_1^{k} \log{t} dt < \log{k!} \\ \frac{\log{(k-1)!}}{\log{k!}} < \frac{\int_1^{k} \log{t} dt}{\log{k!}} < 1 \end{equation}$

十分に大きい $k$ に対して
$\displaystyle \frac{\log{(k-1)!}}{\log{k!}} = 1 - \frac{\log{k}}{\log{k!}} \simeq 1$
である．*1
上式からはさみうちの原理より、
$\displaystyle \frac{\int_1^{k} \log{t} dt}{\log{k!}} \simeq 1$
となる．
よって
$\displaystyle \log{k!}　\simeq \int_1^{k} \log{t} dt$
[補題１証明終]

補題１の結果を元の式に代入数する．
$x ,\, (n-x)$ が十分に大きいとき
$\displaystyle \begin{equation} \begin{split} \log{B(n,p)} &= \log{n!} - \log{x!} - \log{(n-x)!} + x\log{p} + (n-x)\log{(1-p)}\\ &\simeq \log{n!} - \int_1^{x} \log{t} dt - \int_1^{n-x} \log{t} dt + x\log{p} + (n-x)\log{(1-p)} \end{split} \end{equation}$
となる．

この変形によって微分を考えることができて，
一階微分、二階微分はそれぞれ
$\displaystyle \begin{equation} \begin{split} \\(\log{B(n,p)})' &\simeq - \log{x} + \log{(n-x)} + \log{p} - \log{(1-p)} \\ \\(\log{B(n,p)})'' &\simeq - \frac{1}{x} - \frac{1}{n-x} \end{split} \end{equation}$
となる．

$\log{B(n,p)}$ を平均値の周りでTaylor展開する．
ただし、平均値と分散は二項分布の性質から定まる（平均 $\mu = np$ 、分散 $\sigma^2 = np(1-p)$ ）

$\displaystyle \begin{equation} \begin{split} \log{B(n,p)} &\simeq \log{B(x=\mu | n,p)} + (\log{B(x=\mu | n,p)})'(x-\mu) + \frac{1}{2!}(\log{B(x=\mu | n,p)})''(x - \mu)^2 \\ &\simeq \log{B(x=\mu | n,p)} - \frac{1}{2np(1-p)}(x - \mu)^2 \\ &= \log{B(x=\mu | n,p)} - \frac{(x - \mu)^2}{2\sigma^2} \end{split} \end{equation}$

ここで，第一項は定数なので、 $\log{C}$ とおいておく．
（近似の過程で確率密度の制約条件「定義域全域で積分すると１になる」が抜けてしまうため、改めて係数を求める必要がある．）

求める確率分布を $N(x)$ とすると，
$\displaystyle \begin{equation} \begin{split} \log{N(x)} &\simeq \log{C} - \frac{1}{2\sigma^2}(x - \mu)^2 \\ N(x) &\simeq C \exp{\left(-\frac{(x - \mu)^2}{2\sigma^2}\right)} \end{split} \end{equation}$
これで変数部分まで求めることができた．

最後に，
先ほども述べたように，確率密度の制約条件を満たすよう係数を決定しなければいけない．
すなわち，
$\displaystyle \int_{-\infty}^{\infty} N(x) dx = 1$
となる $C$ を求める．

補題として、
[補題2]
$\displaystyle \int_{0}^{\infty} e^{-x^2} dx = \frac{\sqrt{\pi}}{2}$
を示す．（※ガウス積分）
[補題2証明]
$\displaystyle I(R) = \int_{0}^{R} e^{-x^2} dx$
とおくと、証明すべきは
$\displaystyle \lim_{R \to \infty}I(R) = \frac{\sqrt{\pi}}{2}$
である．

$\displaystyle (I(R))^2 = I(R)I(R) = \int_{0}^{R}\int_{0}^{R} e^{-(x^2+y^2)}dxdy$
とおくと，この積分領域は $xy$ 平面上における一辺 $R$ の正方形である．
一方で次のような扇状の積分範囲を定義すると，
$D(R) = \left\{(x,y)\,|\, x\geq 0,\, y \geq 0,\, x^2+y^2 \le R^2 \right\}$
次のような大小関係が成り立つ
$\displaystyle \int\int_{D(R)} e^{-(x^2+y^2)}dxdy < (I(R))^2 < \int\int_{D(\sqrt{2}R)} e^{-(x^2+y^2)}dxdy$

ここで，
$\displaystyle J(R) = \int\int_{D(R)} e^{-(x^2+y^2)}dxdy$
とする．
$\displaystyle \lim_{R \to \infty} J(R) = \frac{\pi}{4}$
となることから，はさみうちの原理より $(I(R))^2 = \sqrt{\pi}/4$ となることを示す．

$J(R)$ を極座標表示に変換して計算する
$x = r\cos{\theta} , \, y = r\sin{\theta} \\ 0 \leq r \leq R ,\, 0 \leq \theta \leq \frac{\pi}{2}$
として，
$\displaystyle \begin{equation} \begin{split} J(R) &= \int_{0}^{R}\int_{0}^{\pi/2} e^{-r^2} r d\theta dr \\ &= \left\{\int_{0}^{R} re^{-r^2} dr \right\} \left\{\int_{0}^{\pi/2} 1 d\theta \right\} \\ &= \frac{\pi}{2}\left[ - \frac{1}{2} e^{-r^2} \right]_{0}^{R} \\ &= \frac{\pi}{4}\left( 1 - e^{-R^2} \right) \end{split} \end{equation}$

$R$ が十分に大きいとき，
$\displaystyle \begin{equation} J(R) = \frac{\pi}{4} \\ J(\sqrt{2}R) = \frac{\pi}{4} \end{equation}$
であることがわかる．

はさみうちの原理より，
$\displaystyle \begin{equation} \begin{split} (I(R))^2 &= \frac{\pi}{4} \\ I(R) &= \frac{\sqrt{\pi}}{2} \end{split} \end{equation}$

が示された．
$\displaystyle \left(\int_{0}^{\infty} e^{-x^2} dx = \frac{\sqrt{\pi}}{2} \right)$
[補題2証明終]

補題２の結果から，係数 $C$ を求める．
$x = \sqrt{2}\sigma X +\mu$
と変数変換することで，
$\displaystyle \begin{equation} \begin{split} \int_{-\infty}^{\infty} N(x) dx &= \int_{-\infty}^{\infty} C \exp{\left(-\frac{(x - \mu)^2}{2\sigma^2}\right)} dx \\ &= \sqrt{2}\sigma C \int_{-\infty}^{\infty} e^{-X^2}dX \\ &= \sqrt{2\pi\sigma^2} C \end{split} \end{equation}$
から，
$\displaystyle C=\frac{1}{\sqrt{2\pi\sigma^2}}$
が求まる．

以上から，
$\displaystyle \lim_{n \to \infty} B(n,p) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)$
となり，二項分布の極限は正規分布に近似されることが証明された．
[証明終]

*1:コメントに証明のあらすじを書いてくれている方がいます。ありがとうございます。

2017-06-23

直下のファイルを走査し一覧表示する [bash, python]

あるディレクトリの直下のファイルに対して巡回しながら処理したい時
シェルスクリプトとpythonでどうするか。

bash

files="./hoge/*"
for filepath in $files; do
  echo $filepath
done

./hoge/1.txt
./hoge/2.txt
のようにディレクトリごと表示される
ファイル名だけ表示したい場合はこう書けば良い

${filepath##*/}

補足

zipファイルの中にzipファイルがあるもの、例えば

a.zip
- nbghuio.zip
- bghjkoi.zip
b.zip
- bhujiko.zip
- qvdshjt.zip

こんな感じのものをまとめて解凍したい時

#!/bin/bash
for zipfile `\find . -name '*.zip'` ; do
    unzip -q ${zipfile}
done

for i in "./*" ; do
    for file in `\find $i -name '*.zip'`; do
        unzip -q -o ${file}
    done
done

こんなスクリプトになる。

Python

import os

directory = "./hoge/"
for root, dirs, files in os.walk(directory):
    for file in files:
        print(file)
        print(root+file)

fileだけの場合は
1.txt
のようになる。rootにディレクトリの文字列があるので
./hoge/1.txt
のようにしたい場合はroot+fileのように書く

技術メモ

役に立てる技術的な何か、時々自分用の覚書。幅広く色々なことに興味があります。

pythonで正規性の検定【コロモゴロフスミルノフ検定（KS検定）】

1標本の場合

試してみる

【補足】KS検定 vs. シャピロ-ウィルク検定

2標本の比較

試してみる

二項分布の極限が正規分布になることの証明【正規近似の証明】

予備知識

証明

方針

証明

直下のファイルを走査し一覧表示する [bash, python]

bash

補足

Python