ブラックショールズモデルでグラフを描く

以前書いたブラックショールズモデルの関数を使って、権利行使までの時間と行使価格を動かしてグラフを描いてみようと思う。
swdrsker.hatenablog.com
権利行使までの時間が長くなるほど緩やかな曲線になるのを見たい。

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import seaborn
seaborn.set_style("whitegrid")

rf_rate = 0.005 #risk free rate (0.5%)
sigma = 0.12 #volatility (12%)
price = 100 #present value

def bs_model(S,x,r,sigma,T):
    d1 = (np.log(S/x) + (r + 0.5 * sigma ** 2)*T)/(sigma*pow(T, 1/2))
    d2 = (np.log(S/x) + (r - 0.5 * sigma ** 2)*T)/(sigma*pow(T, 1/2))
    call = S * stats.norm.cdf(d1) - x * np.exp(-r*T) * stats.norm.cdf(d2)
    put  = x * np.exp(-r*T) * stats.norm.cdf(-d2) - S * stats.norm.cdf(-d1)
    return call,put

リスクフリーレートは0.5%, ボラティリティは12%, 現在価格を100とした。

プットオプション

x = np.arange(75,125)
plt.figure()
for t in [0.01,0.5, 1,2,3]:
    bs = lambda x: bs_model(price,x , rf_rate, sigma, t)[1]
    plt.plot(x, np.vectorize(bs)(x), label="t: %1.1f"%t)
plt.xlabel("Strike Price")
plt.ylabel("Option Premium")
plt.title("Put option (price:100)")
plt.legend()

コールオプション

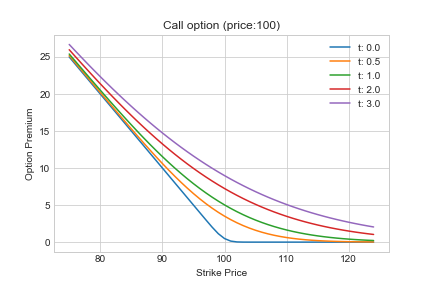
x = np.arange(75,125)
plt.figure()
for t in [0.01,0.5, 1,2,3]:
    bs = lambda x: bs_model(price,x , rf_rate, sigma, t)[0]
    plt.plot(x, np.vectorize(bs)(x), label="t: %1.1f"%t)
plt.xlabel("Strike Price")
plt.ylabel("Option Premium")
plt.title("Call option (price:100)")
plt.legend()