ブラックショールズモデルを解説してみる（ブラックモデル編）

前回は株価モデルを中心に、株価の値動きの前提になっている条件からそれをシミュレーションに落とし込むまでの流れを解説した。
今回は前回の株価モデルの話をもとにしてブラック・ショールズ方程式の概念的な解説をしていく。
まずそもそもブラック・ショールズ方程式というのは何を求めるためのものなのかを解説した後、
数式で言われている結果がシミュレーションの結果と相違ないことを確認していく。

↓前回の記事
swdrsker.hatenablog.com

ブラックショールズ方程式は何を求めるものなのか？

ブラックショールズ方程式は何を求めているのかを説明する前にまずオプション取引について紹介しなければいけない。

オプション取引とは

オプション取引とは「T年後にK円で買う権利」や「T年後にK円で売る権利」を売り買いすること。
（売買の対象は株・通貨・国債・金利などさまざま。）
例えば、

2年後にドルを1ドル140円で10万ドル買う権利をあげますよ

というのがオプションだ
2年後に今のように1ドル145円になっていればその時点では50万円分の価値があることになる。
逆に再びリーマンショックが起こって1ドル80円になってたとしても、権利を行使せずに買わなければ良いだけなのでその時点での価値は0円ということだ。

T時点での1ドル価格をして数式で表すと

T時点の価格より行使価格が高ければその差額だけ儲かることになるし、T時点の価格が行使価格を下回れば権利を手放すので価値はゼロになる。

T時点のことを「満期日」あるいは「権利行使日」、K円のことを「行使価格」と呼ぶ。
また買う権利のことを「コールオプション」と呼び、売る権利のことを「プットオプション」と呼ぶ。
ここではわかりやすいようにコールオプションを前提として説明する。

オプション取引の価格は？

ここで問題になるのがこの取引の値段だ。
オプションの値段*1がいくらなら買う側も売る側も納得できるか？
これを理論的に導いたのがブラックショールズ方程式ということである。

もう少し詳しく

ブラックショールズ方程式のエッセンスを簡単に紹介する。

T年後に株をK円で買う権利

というコールオプションを考えよう。
現時点から見た権利行使日における株価の値段xの確率分布をとすると
権利行使日時点の価値はこのように表せる。

これを現時点での価値で表す。
株価モデル編で説明したように、資産は持っているだけで利息が付くもので、これをリスクフリーレートと呼んだ。
オプションの価値もそれと同じようにリスクフリーレートで利息が付く。
権利行使日時点のオプション価値は利息が付いた後の価格と考えられるので、現時点の価値を考えるにはその分だけ割り引く必要がある。
前回の最後に解説した連続金利の考え方を用いると、
現時点で円の価値のあるものはT年後には円の価値になる。
裏を返せばT年後に円の価値があるものは現時点では円の価値ということである。
オプションの価格も同様に、現時点での価値は

となる。
今は不明であるが、ここで示したようなオプションの現在価値を株価モデルの仮定のもとに理論的に計算したのがブラック・ショールズ方程式になる。

シミュレーションによる確認

それではここまでの話をシミュレーションで確認してみる。
株価モデルについては前回のものを用いる。

↓前回の株価モデルのコード

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import seaborn
seaborn.set_style("whitegrid")

size_t = 1200 #1200日
dw = np.random.randn(size_t)
price = np.zeros(size_t)
rf_rate = 0.01 #リスクフリーレート(年利1％)
sigma = 0.12 #ボラティリティ(12%)
price[0] = 100 #初期値
for i in range(1, size_t):
    price[i] = price[i-1] * (1 + rf_rate / 360 + sigma * dw[i] / np.sqrt(360)) 

plt.plot(price)
plt.show()

方針

ここで

今100円の株を3年後1株100円で買う権利の値段

を考える。

最終的な株価がわかっている時、
そのオプションの価値は

であった。
これを現在価値に戻すと

となる。
シミュレーションを繰り返し、このの平均を取ることでオプションの現在価値を割り出してみる。

実装

では早速実装してみる。

import math
import numpy as np
import matplotlib.pyplot as plt
from statistics import mean
import seaborn
seaborn.set_style("whitegrid")

# リスクフリーレート
rf_rate = 0.01
# ボラティリティ
sigma = 0.12
# 初期株価
init_price = 100
# 権利行使価格
strike_price = 100
# 満期日
maturity_duration = 365 * 3

# 株価モデルのパス生成
def generate_path(days, rf_rate, sigma, init_price):
    size_t = days
    dw = np.random.randn(size_t)
    price = np.zeros(size_t)
    price[0] = init_price
    for i in range(1, size_t):
        price[i] = price[i-1] * (1 + rf_rate / 365 + sigma * dw[i] / np.sqrt(365)) 
    return price

# 現在価値の計算
def present_value(final_price, days, rf_rate):
    return np.exp(-rf_rate * days/365) * max(final_price - strike_price, 0)

N = 3000 # シミュレーション回数
x = range(0, N, 10)
y = []
result = []
for i in range(N):
    final_price = generate_path(maturity_duration, rf_rate, sigma, init_price)[-1]
    pv = present_value(final_price, maturity_duration, rf_rate)
    result.append(pv)
    if i % 10 == 0:
        y.append(mean(result))
print(f"present value: {y[-1]}")        
plt.xlabel("Simulation Num")
plt.ylabel("Present Value of Call Option")
plt.plot(x,y)
plt.show()

実行結果

present value: 9.683538793313692

3000回のシミュレーションではオプションの現在価値は9.68円となった。

検証

それでは、実際のブラック・ショールズ方程式の解析解で検証してみる。
解説しだすと長ったらしくなるのであえて解説はしないが、
ブラックモデルの解析解は以下のようになる。
swdrsker.hatenablog.com

import numpy as np
from scipy import stats
def bs_model(S,x,r,sigma,T):
    d1 = (np.log(S/x) + (r + 0.5 * sigma ** 2)*T)/(sigma*pow(T, 1/2))
    d2 = (np.log(S/x) + (r - 0.5 * sigma ** 2)*T)/(sigma*pow(T, 1/2))
    call = S * stats.norm.cdf(d1) - x * np.exp(-r*T) * stats.norm.cdf(d2)
    return call

print(bs_model(100, 100, 0.01, 0.12, 3))

実行結果

9.716855499608009

シミュレーションの結果と概ね一致している事が検証できた。

まとめ

ここではブラック・ショールズ方程式が何をしたいのか。なにを目指した方程式なのかという解説をした。
一言で言えば「オプションのプライシング」ということになるが、
それが具体的にどういうことなのかをシミュレーションで実験し検証した。

suzuri.jp

*1:オプションプレミアムという

シェルスクリプトでFOR文でバックグラウンドで起動したの並列処理を待機する方法

# ジョブ ID を格納する配列
job_ids=()

array=(2 5 4 7 2 1)
for i in ${array[@]}; do
    
    # ジョブをバックグラウンドで実行し、ジョブ ID を取得
    (sleep $i && echo $i) &
    
    # 直前にバックグラウンドで起動したプロセスの ID を取得
    job_ids+=($!)
done

# すべてのジョブが終了するまで待機
for job_id in "${job_ids[@]}"; do
    wait "${job_id}" || exit 1
done

# 後続処理を記述
echo "Finish!"

結果

 » sh sample.sh
1
2
2
4
5
7
Finish!

■例
あるフォルダのすべてのファイルに対して並列で時間のかかる処理を実行し、並列処理が完了したら後続処理をしたいという場合

input_dir=$1

# ジョブ ID を格納する配列
job_ids=()

for file in "${input_dir}/*"; do
    
    # first.sh(時間がかかる処理)をバックグラウンドで実行し、ジョブ ID を取得
    (sh first.sh "${file}") &
    
    # 直前にバックグラウンドで起動したプロセスの ID を取得
    job_ids+=($!)
done

# すべてのジョブが終了するまで待機
for job_id in "${job_ids[@]}"; do
    wait "${job_id}" || exit 1
done

# 後続処理を記述
sh second.sh

補足

job_ids=()

この書き方ではbash特有の記法になる。
POSIX準拠の記法は以下のようになる。

# POSIXシェルでは配列を使わず、代わりに一時ファイルを使用
job_ids_file=$(mktemp)

for file in "${input_dir}/*"; do
    # first.sh(時間がかかる処理)をバックグラウンドで実行し、ジョブ ID を一時ファイルに書き込む
    (sh first.sh "${file}") &
    echo $! >> "$job_ids_file"
done

# 生成したジョブIDの一覧を読み込み、それぞれのジョブが終了するのを待つ
while IFS= read -r job_id; do
    wait "${job_id}" || exit 1
done < "$job_ids_file"

# 一時ファイルを削除
rm "$job_ids_file"

# 後続処理を記述
sh second.sh

【DRF】 カスタムユーザーを使ってuserをregisterする時、パスワードを入れているのに「この項目は必須です。」と言われる

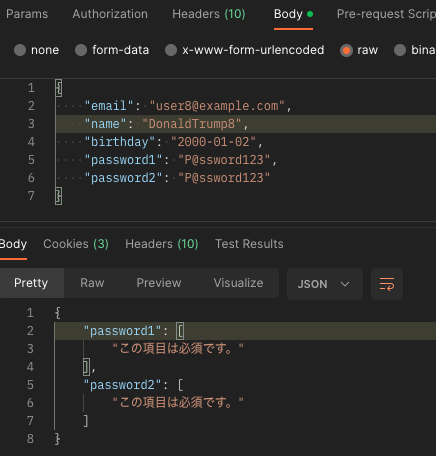
Django Rest Frameworkを使ってカスタムユーザーを使ってユーザー登録しようとした時、password1とpassword2を同じにして登録しているはずなのにパスワードが必須だと言われる。

{
    "password1": [
        "This field is required."
    ],
    "password2": [
        "This field is required."
    ]
}

（日本語版）

{
    "password1": [
        "この項目は必須です。"
    ],
    "password2": [
        "この項目は必須です。"
    ]
}

ネットでいくら探しても有力な解決法はなかったけれど、自分なりの解決法が見つかったのでブログに記すことにする。
qiita.com
一応Qiitaでも同様の現象が報告されているが解決策が力技すぎた。
当記事の原因とは違うなどどうしても解決できない場合は参考にしてみてほしい。

前提

認証には dj-rest-auth を使用。
今回作成したカスタムユーザーは以下の通り。

[accounts/models.py]

...
class User(AbstractBaseUser, PermissionsMixin, TimeStampedModel):
    name = models.CharField(max_length=128, verbose_name=_('Name'), null=False, blank=True)
    email = models.EmailField(unique=True, verbose_name=_('Email'))
    icon = models.ImageField(verbose_name=_('Profile picture'), null=True, blank=True)
    birthday = models.DateField(verbose_name=_('Birthday'), null=True, blank=True)
    bio = models.TextField(verbose_name=_('Biography'), null=True, blank=True)

    is_active = models.BooleanField(verbose_name=_('Is active'), default=True)
    is_staff = models.BooleanField(verbose_name=_('Is staff'), default=False)
    is_superuser = models.BooleanField(verbose_name=_('Is superuser'), default=False)

    objects = CustomUserManager()

    USERNAME_FIELD = 'email'

[accounts/serializers.py]

....
class UserRegisterSerializer(RegisterSerializer):
    email = serializers.EmailField()
    name = serializers.CharField(max_length=128)
    birthday = serializers.DateField()
    bio = serializers.CharField(required=False)

    def get_cleaned_data(self):
        return {
            'username': self.validated_data.get('username', ''),
            'password1': self.validated_data.get('password1', ''),
            'email': self.validated_data.get('email', ''),
            'name': self.validated_data.get('name', ''),
            'birthday': self.validated_data.get('birthday', None),
            'bio': self.validated_data.get('bio', None),
        }

    def custom_signup(self, request, user):
        data = self.cleaned_data
        user.name = data.get('name', '')
        user.birthday = data.get('birthday', '')
        user.bio = data.get('bio', '')
        user.save()

modelsとserializersはこのように定義し、settingsでこのserializerをregisterに使うように設定した。

[project_name/settings.py]

...
REST_AUTH = {
    "REGISTER_SERIALIZER": "accounts.serializers.UserRegisterSerializer",
}
...

ここまでの流れはだいたいこの記事の通りにした
Custom users using Django REST framework | Kraken Systems Ltd.

原因

原因は自分の場合、JSONの出力と入力をcamelCaseに対応させるため djangorestframework_camel_case を入れていたことが問題だった。
どうやら "password1" が "password_1" と解釈されるよう。
"password1"って書き方正式にはsnake_caseじゃないんですね。知らなかった…
この原因を突き止めるまで相当苦労した…

解決

暫定対応１

とりあえずcamelCaseを辞めるのを暫定対応とした。
つまり `settings.py` を書き換える。

REST_FRAMEWORK = {
    'DEFAULT_RENDERER_CLASSES': (
        'djangorestframework_camel_case.render.CamelCaseJSONRenderer',
        'djangorestframework_camel_case.render.CamelCaseBrowsableAPIRenderer',
        'rest_framework.renderers.JSONRenderer',
    ),
    'DEFAULT_PARSER_CLASSES': (
        'djangorestframework_camel_case.parser.CamelCaseFormParser',
        'djangorestframework_camel_case.parser.CamelCaseMultiPartParser',
        'djangorestframework_camel_case.parser.CamelCaseJSONParser',
        'rest_framework.parsers.JSONParser',
    ),

こう書いていたのを

REST_FRAMEWORK = {
    'DEFAULT_RENDERER_CLASSES': (
        'rest_framework.renderers.JSONRenderer',
    ),
    'DEFAULT_PARSER_CLASSES': (
        'rest_framework.parsers.JSONParser',
    ),

こうする。

暫定対応２

とはいえフロントとの疎通の仕様上いまさらcamelCaseをsnake_caseに書き換えるのは無謀な話ということだった。
なのでどうにかならないかと思い悩んだ結果Serializerを書き換えることでなんとか対応できた。
具体的にはpassword1とされるところを徹底的にpassword_1に置き換えるという作業をした。

• 継承元のserializers.Serializerでfieldの変数名を解釈している箇所"fields"
• RegisterSerializerで"password1", "password2"という変数名を取って来て比較している箇所"validate"
• RegisterSerializerで"password1"というフィールドを取得する箇所"get_cleaned_data"

を書き換える必要があった。

from django.utils.functional import cached_property

class UserRegisterSerializer(RegisterSerializer):
    email = serializers.EmailField()
    name = serializers.CharField(max_length=128)
    birthday = serializers.DateField()
    bio = serializers.CharField(required=False)

    @cached_property
    def fields(self):
        from rest_framework.utils.serializer_helpers import BindingDict
        fields = BindingDict(self)
        for key, value in self.get_fields().items():
            if key == "password1":
                key = "password_1"
            if key == "password2":
                key = "password_2"
            fields[key] = value
        return fields

    def validate(self, data):
        if data['password_1'] != data['password_2']:
            raise serializers.ValidationError(_("The two password fields didn't match."))
        return data

    def get_cleaned_data(self):
        return {
            'username': self.validated_data.get('username', ''),
            'password1': self.validated_data.get('password_1', ''),
            'email': self.validated_data.get('email', ''),
            'name': self.validated_data.get('name', ''),
            'birthday': self.validated_data.get('birthday', None),
            'bio': self.validated_data.get('bio', None),
        }

    def custom_signup(self, request, user):
        data = self.cleaned_data
        user.name = data.get('name', '')
        user.birthday = data.get('birthday', '')
        user.bio = data.get('bio', '')
        user.save()

継承元のserializers.Serializer の関数をオーバーライドするという魔改造なのでDjangoの仕様が変わるとそれに対応できなくなるという怖さがある。

追記

恒久対応

ついに恒久対応を見つけてしまった。
djangorestframework_camel_caseの仕様で特定の文字をparse対象から省くことができる機能がある。
GitHub - vbabiy/djangorestframework-camel-case: Camel case JSON support for Django REST framework.

[project_name/settings.py]

REST_FRAMEWORK = {
    # ...
    "JSON_UNDERSCOREIZE": {
        "ignore_keys": ("password1", "password2"),
    },
    # ...
}

とするだけ。
※ accounts/serializers.pyは元に戻す